The Hall effect
This effect was discovered by Edwin Hall in 1879 using a
strip of gold foil. He showed that a p.d. could be built up across a conductor in a magnetic field
when an electric current is passed through it.
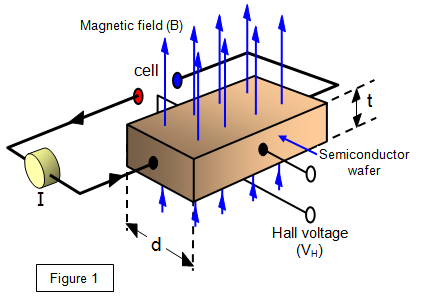
The sign of the charge carriers in a given material can be found using
the Hall effect. A specimen of the material has a small current passed through it while it is
placed in a magnetic field so that the field acts at right angles to the face of the specimen (see
Figure 1).
The magnetic field will exert a force on the charge carriers so that they move to
one side of the specimen or the other. This will build up a potential difference across the
material which will just balance the magnetic force at equilibrium.
The sign of the potential will
determine whether the charge carriers are positive or negative.
Consider a region
where an electric field of intensity E and a magnetic field of intensity B act at right angles to
each other. If an electron moves in that region at right angles to both fields and we adjust the
strength of the fields so that the forces on the electron due to the two fields are equal and
opposite then:
eE = eV/d = Bev
In the Hall
effect the electrons move in the magnetic field towards one side of the specimen so creating the electric
field and this movement continues until the electric filed produced is just sufficient to balance the force
due to the magnetic field (B).
The voltage across the specimen at that point is called the Hall voltage
(VH) and is given by the equation:
eVH/d = Bev
Therefore, since I = nAve where n is the number of charge
carriers per cubic metre and A the cross-sectional area of the specimen, d its width and t its
thickness,
Hall voltage (VH) = BI/net
The value of the Hall
voltage (VH) depends on the current, flux density, electron charge and thickness of the specimen.
It also depends on n. The more free charge carriers there are in the material, the smaller the
Hall voltage will be.
For a metal such as copper n = 1029 and the hall voltage will
be only 0.06 micro-volts for B = 1T, I = 1A and t= 1mm. For semiconducting materials n =
1025 and so a voltage of 0.6 millivolts is produced.
Example problem
A slice of semi conducting material 0.5 mm thick is placed at right angles to a magnetic field of flux density 0.05 T. If a Hall voltage of 0.3 mV is generated across the specimen when a current of 100 mA flows though it calculate the number of free electrons per cubic metre of the specimen.
VH = BI/net and so
n = BI/ VHet = 0.05x100x10-3/[0.3x10-3x1.6x10-19x0.5x10-3] = 2.1x1023 m-3
A Hall probe may be used to find the number or sign of the
charge carriers or to measure the flux density of a steady magnetic field.
The quantity 1/ne is known as the Hall coefficient for a
material.