Ramp generator

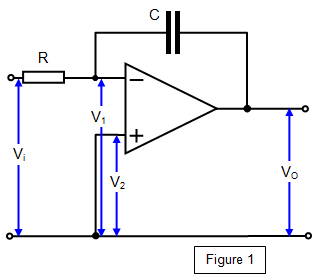
If the feedback resistor of the inverting voltage amplifier is replaced by a capacitor, as shown in Figure 1, a ramp generator or integrator is formed.

If the input voltage V₁ is constant and RC = 1 s, then the output voltage V_o after a time t is given by V_o = V_it

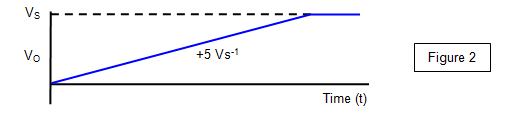
This means that the output voltage rises steadily with time (hence the name of ramp generator). This increase continues until the op amp saturates at a voltage just less than the supply voltage.

The variation of the voltage output against time is shown in Figure 2 (this shows a rate rise of potential difference of 5 Vs^-1). Since P is almost zero (a virtual earth) the voltage across the input resistor R will be the input voltage V1 and the voltage across the capacitor C will be the output voltage V_o. If we assume that no current flows into the inverting input of the op amp, then all the input current I flows to the capacitor C and so charges it up.

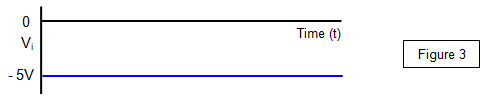
If V₁ is constant then I will be constant (see Figure 3), and its value will be given by I = V_i/R
C therefore charges at a constant rate.

If Q is the charge on C at a time t and if the potential difference across it changes from 0 to V_o in that time, then (since I is constant) Q = V_oC = It

Therefore combining this with the equation above gives: -V_oC = V_it/R or - V_o = [1/RC]V_it

If C and R are chosen such that CR = 1 then:

Output voltage of the ramp generator (V_o) = V_it

A more general case is where V₁ varies and then:

V_o = -[1/RC]∫V_idt

This last equation is the reason why this circuit is also known as an integrator, since the value of V₁ is integrated over a certain time interval. This type of circuit will be found in most oscilloscopes as a means of producing the steadily rising voltage needed for the time base. The ramp generator is also used in the digital voltmeter, the analogue to digital converter and in digital recording.