Equations of motion
In studying the motion of objects it is
often helpful to use an equation to work out the velocity, acceleration or the
distance travelled.
We use the following letters to represent certain
quantities:
Distance travelled s
measured in metres (m)
Time taken
t measured in seconds (s)
The velocity at the start (called
initial velocity) u measured in m/s
The velocity at the end (called the
final velocity) v measured in m/s
The acceleration of the object
a measured in m/s
21. Non accelerated
motion – that is motion at a constant
velocity
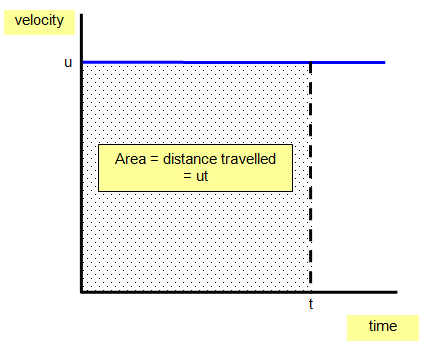
The area
under the line of the velocity –time graph is the distance travelled by the
object in the time t.
For example u = 20m/s and t = 300 s
Distance (s) = ut = 20 x 300 = 6000 m
The equation for non accelerated
motion is:
2.
Accelerated motion - constant acceleration
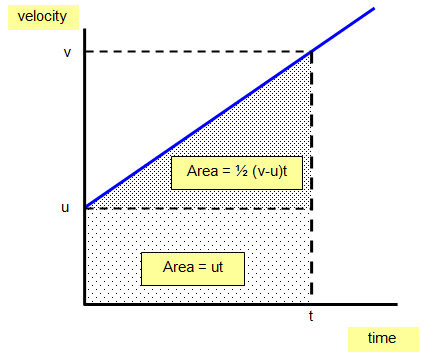
Distance travelled = area under the line =
ut + ½ (v-u)t
But acceleration = (v-u)/t and so (v-u) = at
therefore:
Distance travelled (s) = ut + ½ (v-u)t = ut + ½ [at]t = ut +
½ at
2
If
the object starts from rest u = 0 and so the equation becomes:
Another
useful equation is:
Remember that these equations onlt apply when the acceleration of the object is
CONSTANT.
USING EQUATIONS
This
section is designed to help you work out some of the problems using the equations of motion.
If you need to use any of these equations to
work out problems the way to do it is this:
(a) write down what you are given, usually
three things
(b) look for the equation that contains these three things and the quantity that
you are trying to find
(c) put the numbers in the
CORRECT equation and work it
out
You will need to know how to rearrange equations to make different quantities the
subject of the equation.
You might like to try using the triangle rule if there are only
three quantities in the equation but some of them are more complex than this.
