
Think of a space probe on a journey to Neptune. On
its way it will have to pass Jupiter – the largest planet in the Solar System.
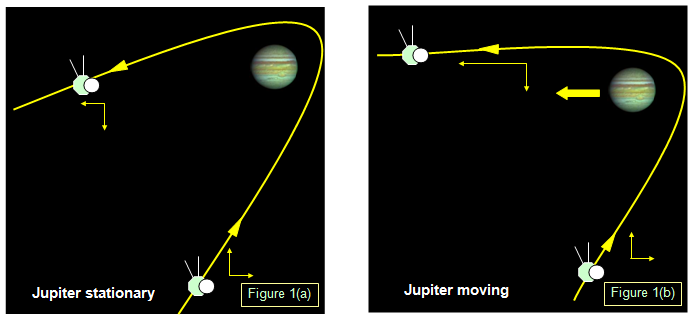
Imagine first
that Jupiter is at rest. As the probe nears Jupiter it accelerates because of the gravity pull of
the planet. It swings round Jupiter and moves away slowing down as it does so. Assuming
that there is no energy lost the speed of the space probe will be same at equal distances
from Jupiter before and after the encounter. Not a lot of use if we are trying to give the space
probe some extra energy.
However Jupiter is not stationary! It is moving in its orbit
around the Sun at about 48000 km/hr. (See Figure 1(b)). As it space probe moves towards
the planet it will accelerate as before but because Jupiter is moving it is "dragged along" by
the planet, having its speed increased considerably by the planets motion. Its speed after the
encounter is much greater than it was before. The gravity pull of the planet has given the
space probe some additional energy. Of course the gravity pull of the space probe will have
slowed down Jupiter but by only a tiny amount because the planet is so much more massive
than the space probe.
The space probe will have had its speed in the direction of
Jupiter's motion increased greatly. It has gained energy from the planet.
To get the
best gravity effect or slingshot it is vital to launch the space craft at the right time so that it
gets the slingshot effect in the right direction, hurling it towards its destination rather than
whipping it out away from the Solar System into deep space.
It is thought that the
gravity assist of Jupiter in the past may have been responsible for protecting the Earth from
some asteroid collisions.
A little maths
If you think
about the velocity vectors in Figure 1(b) you can see that the vector in the direction of motion
of the planet has been increased by an amount almost equal to the velocity of the planet.
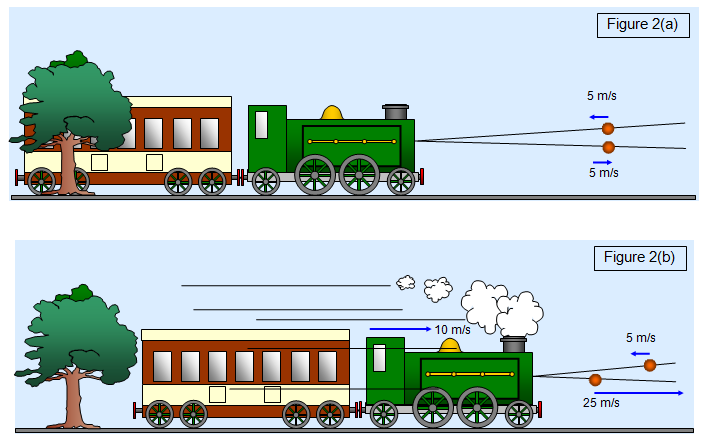
Case (a) the ball
rebounds from the train (not losing any energy in the collision) and moves back at 5
m/s.
Case (b) now assume that the train is moving from left to right at 10 m/s. The
ball moves at 5 m/s relative to the ground (that is 15 m/s relative to the train). It hits the train
and rebounds at 15 m/s relative to the train. But the train is moving at 10 m/s relative to the
ground and so the ball rebounds at 15+10 = 25 m/s relative to the ground.
The ball
has gained kinetic energy from the train.
