Distance measurement in Astronomy
Being able to measure the
distances of astronomical objects is very important in our understanding of the scale of the
Universe.
Radar
The distance from the Earth of objects in the Solar
System can be measured using radar. A pulse is sent out and the time taken for the reflected
pulse to be received is recorded. Knowing the speed of radar in free space and the time
between transmission and reception the radar pulse enables us to find the distance of the
object.
For example the time between the radar pulse being sent out and the
reflected pulse being received would be 2.5 s for the Moon and up to 50 minutes for Jupiter
and around five and a half hours for Pluto. (The last two numbers depend on the relative
positions of the Earth, Jupiter and Pluto in their orbits)
For objects outside the solar
system other methods have to be found.
Parallax
You can find the
distances of stars that are 'relatively close' to the Earth using parallax.
A very simple
example of parallax is to hold one forefinger upright about 30 cm in front of your nose and
close your right eye. Using just your left eye line up your forefinger with an object on the
other side of the room. Now open your right eye and close your left eye. Your finger appears
to move against the background.
To understand exactly what is meant by parallax
go and stand at one end of the lab, you will be the observer. Now get one member of your
class to stand at A in the middle of the lab (they represent a star that is close to the Earth
and we will call them the 'nearby star') and some others to stand at the far end (they
represent distant stars). Look the 'nearby star' and see which of the 'distant stars' lie in line
with it (See Figure 1).
Now walk across the lab to Position 2 and check again which
of the 'distant stars' is in line with the 'nearby star ', you will see that the apparent position of
the 'nearby star' compared with the distance stars has changed.

The angle between the two directions in positions 1
and 2 is 2P, and half that angle is called the PARALLAX (P) of the 'nearby star'.
Now
look at the 'nearby star' when it is in position B. The parallax here is Q and you can see two
things about the 'nearby star' now:
(a) it is further away from the observer
(b) the
parallax of the star is smaller than that of the 'star' at A
Figure 2 shows the use of
parallax to measure the distance of an actual star – say Alpha Centauri. This time the 'base line'
is the diameter of the Earth's orbit – in other words a line joining the position of the Earth at
two points six months apart.

The
direction of Alpha Centauri is measured against the background of the distant stars at the two
points P
1 and P
2. The angle 2A is measured and so the parallax (angle A) can be found.
If you know the angle A and the radius of the Earth's orbit (R) you can find the
distance of the star (D). Stars that are close to the Earth clearly have a larger parallax than
ones far away.
Even nearby Stars are so far away that their direction changes only
slightly against the background of the distant stars when seen from points on the Earth's orbit
six months apart.
Nearby stars have a parallax of only a fraction of a second of arc
(one second of arc is 1/3600 of a degree).
In the example shown Alpha Centauri (distance
4.3 light years) has a parallax of 0.75 " of arc.
A more distant star such as Spica in
the constellation of Virgo, which is 220 light years away, has a parallax of only
0.023".
The Parsec
Astronomers use the parallax of the
star to define a new distance unit called the PARSEC.
1 parsec is the distance of an object which has a parallax of 1” of arc. This means that it subtends an angle of one second using the radius of the Earth’s orbit as the baseline.
The radius of Earth's orbit = 1.5x10
11 m and therefore if
the
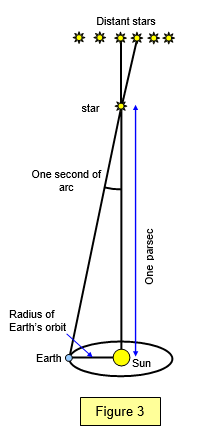
parallax of a star is 1" the distance can be found
from:
tan(1") = 1.5x10
11/d so d = 3.06 x10
16 m (See Figure 3)
Distances
between galaxies are usually measured in millions of parsecs or Mega parsecs
(Mpc).
1 parsec = 3.06x1016 m = 2.04x105 AU = 3.26 light years
1 Mega parsec = 3.06x1022 m = 2.04x1011 AU = 3.26x106 light years
The parallax of
a number of stars is shown in the following table.
| Star |
Parallax
(" of arc) |
Distance (l.y) |
|
Star |
Parallax
(" of arc) |
Distance (l.y) |
| a Centauri |
0.750 |
4.3 |
|
Vega |
0.133 |
25 |
| Barnard's star |
0.545 |
6.0 |
|
Arcturus |
0.097 |
34 |
| Sirius |
0.377 |
8.6 |
|
Aldebaran |
0.054 |
60 |
| Procyon |
0.285 |
11.4 |
|
Adhara |
0.067 |
570 |
At distances much greater than this the parallax method becomes impossibly difficult to
measure. Remember that 1" of arc is the angle subtended by a human head almost ¾ of a
kilometre away. Therefore the parallax of Castor is the same as the angle subtended by a
human head at a distance of almost 750 km!
A VERSION IN WORD IS AVAILABLE ON THE SCHOOLPHYSICS USB