

When an
object is balanced on a pivot the turning effect of the forces on one side of the pivot must
balance the turning effect of the forces on the other side of the pivot - if they didn't it would
not balance.
In the picture (Figure 1(a) two girls are sitting on a see saw. They have
moved until it is balanced. They are the same weight and so to balance the see saw they
must sit the same distance from the pivot.

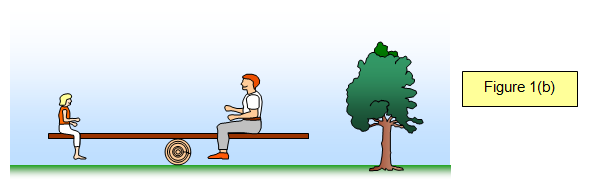
In the picture (Figure 1(b) one of the girls gets off and a man sits on instead. They move until the see saw is balanced. The girl is much lighter than the man and so she has to sit further away from the pivot then he does so that she can balance his extra weight.
You
should remember that the turning effect of a force is called the moment of the force and is
found by multiplying the force by its distance from the pivot. When the see saw is balanced
we say that the anticlockwise moments (those trying to turn the object anticlockwise) equal
the clockwise moments (those trying to turn the object clockwise). In our example the man's
weight tries to turn the see saw clockwise and the girl's weight tries to turn it
anticlockwise.
You can investigate this in the lab by using sets of weights hanging
on a wooden ruler (Figure 2)