Relation between g and G
Using F = ma we know that the force on a mass m at a point where the
gravitational intensity of a planet is g is mg.
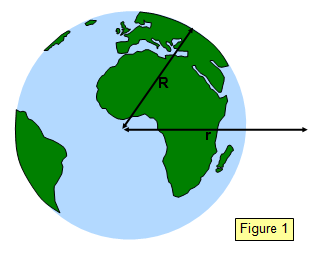
But this force is also given by F = GMm/r2
where M is the mass of the planet and r is the distance from its centre (See Figure 1).
So
F = mg = GMm/r2 and therefore
g = GM/r2
If we think about the surface of the planet then
g = g
o and
r = R and so:
Surface gravity (go) = GM/R2
Weight
What we call the weight of an object at the
Earth's surface (mg
o) can also be expressed as GMm/R
2
Example problem – mass of the Earth
Knowing go = 9.8 ms-2 and that the radius of the Earth is 6.4x106 m and G = 6.67x10-11 Nm2kg-2 we can find the mass of the Earth.
Using M = goR2/G = 9.8x(6.4x106)2/6.67x10-11 = 6.0x1024 kg
Density of a planet and its surface gravity
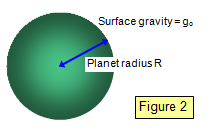
We know that the surface gravity (g
o) of a planet is
given by the formula:
g
o= GM/R
2 but the density of the planet (ρ) =
M/[4/3πr
3] and so
Surface gravity (go) = G4πRρ/3
Example problems
1. Calculate the surface gravity for an asteroid with a radius of 500 m and of the same average density as the Earth(5500 kgm-3)
Surface gravity (go) = G4pRρ/3 = 6.67x10-11x4xπx500/3 = 7.7 x 10-4 ms-2 = 0.77 mms-2
2. Calculate the value of g at the surface of a planet of mass 1018 kg (about one millionth that of the Earth) and radius 60 km. (use G = 6.67x10-11 Nm2kg-2)
g = GM/R2 = 6.67x10-11x1018/(60x103)2 = 0.019 ms-2 = 1.9 cms-2
A VERSION IN WORD IS AVAILABLE ON THE SCHOOLPHYSICS USB