Electrons in a box

If the electron is confined to move in one dimension within the box then the de Broglie waves associated with the electron will be standing waves. Since the wave must have zero value (i.e a node) at the walls of the box only waves that have a wavelength (λ)) = 2L/n are allowed. L is the length of the box and n is a positive integer.

The de Broglie wavelength (λ) of an electron of mass m_e travelling with velocity v = h/m_eλ, where h is Planck’s constant.

The kinetic energy of the electron = ½ m_ev².

Kinetic energy = ½[mv²] = ½[m_e(h/λ) m_e)²] = ½[m_e(nh/2Lm_e)²] = ½[n²h²/4m_eL²] = n²h²/8m_eL²

The potential energy inside the box will be zero and so the expression for the kinetic energy of the electron is actually the total energy of the electron.

You can see from the equation that the energy of the electron is quantised – the only possible values are with n = 1, 2, 3 etc. This means that the energy levels can have values h²/8m_eL², 4h²/8m_eL², 9h²/8m_eL², 16h²/8m_eL² and so on.

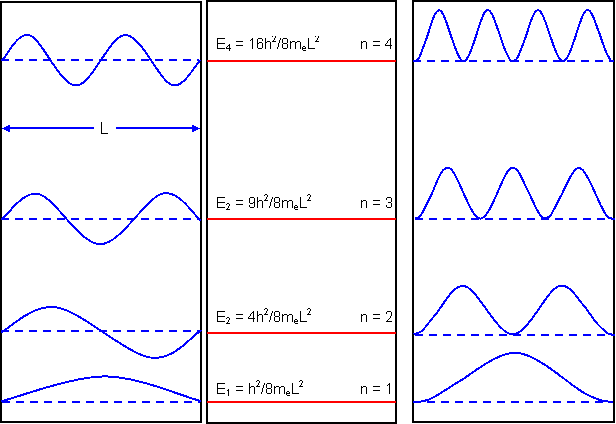
Examples of waves fitting into a box, the energy levels and the probability functions are shown above for n=1,2,3 and and 4. We have assumed the amplitude of the wave associated with the electron to be sinusoidal and the probability of the electron being at a particular point to be proportional to the amplitude of the wave squared. This follows from Schrödinger’s wave equation.